Sistem Koordinat 3 Dimensi

Sistem koordinat tiga dimensi (3D) memungkinkan kita untuk menggambarkan posisi titik dalam ruang. Tidak seperti sistem dua dimensi (2D) yang menggunakan dua sumbu (x dan y), sistem 3D melibatkan tiga sumbu yang saling tegak lurus: sumbu-x, sumbu-y, dan sumbu-z. Sumbu-z ini memberikan dimensi tambahan yang memungkinkan kita menggambarkan ketinggian atau kedalaman dalam ruang.

Konsep Pembagian Wilayah: Oktan

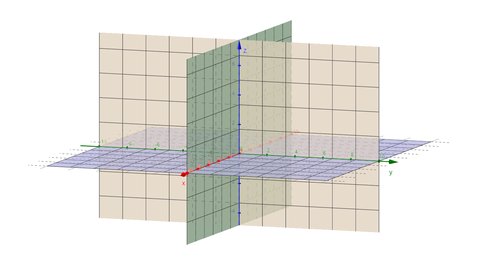
Dalam sistem koordinat dua dimensi, kita mengenal empat kuadran, yang merupakan hasil pembagian oleh sumbu-x dan sumbu-y. Pada sistem koordinat tiga dimensi, ruang dibagi menjadi delapan wilayah yang dikenal sebagai oktan. Oktan adalah hasil dari pembagian oleh ketiga sumbu (x, y, dan z), yang masing-masing bisa bernilai positif atau negatif.

Setiap oktan merepresentasikan kombinasi tanda positif dan negatif dari ketiga sumbu tersebut. Misalnya:

• Oktan pertama adalah wilayah di mana semua nilai koordinat x, y, dan z positif.
• Oktan kedua memiliki nilai x negatif, tetapi y dan z positif.
• Dan seterusnya hingga kita mencakup semua kombinasi.

Pembagian ini membantu kita mengidentifikasi secara tepat di mana sebuah titik berada di ruang tiga dimensi. Misalnya, titik berada di oktan keempat karena nilai x dan y positif, tetapi z negatif.

Komponen Titik pada Sistem Koordinat

Untuk lebih memahami bagaimana posisi titik bekerja dalam ruang tiga dimensi, mari kita perhatikan bagaimana sebuah komponen koordinat berubah dalam berbagai dimensi.

Misalkan :

• Dimensi 1: Jika hanya satu sumbu yang digunakan (misalnya ), maka hanya merepresentasikan satu titik di sepanjang sumbu-x. Ini adalah titik spesifik di mana , tanpa mempertimbangkan sumbu lain.

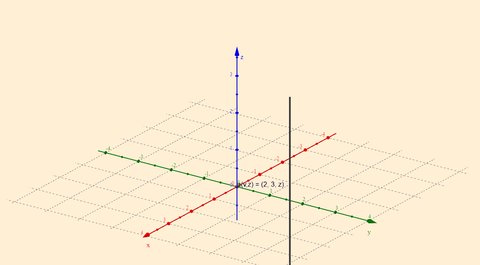
• Dimensi 2: Ketika kita menambahkan sumbu-y dan mempertahankan , posisi ini sekarang membentuk sebuah garis vertikal yang sejajar dengan sumbu-y. Setiap nilai memungkinkan titik tetap berada pada garis ini dengan tetap konstan.

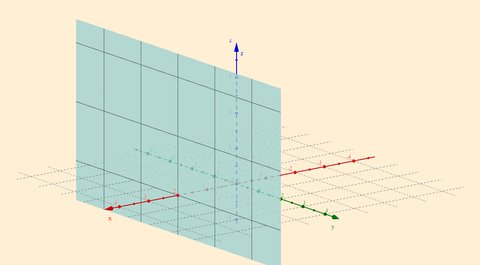
• Dimensi 3: Dalam tiga dimensi, dengan , kita sekarang memiliki bidang yang sejajar dengan sumbu-y dan sumbu-z, yang dikenal sebagai bidang . Bidang ini mencakup semua nilai dan , sementara tetap konstan.

Hal yang sama berlaku untuk komponen y dan z:

• 1 komponen titik akan membentuk sebuah bidang, karena dua sumbu lainnya bisa bervariasi tanpa batas.
• 2 komponen titik akan membentuk sebuah garis, karena hanya satu sumbu yang bervariasi.
• 3 komponen titik akan menunjukkan posisi spesifik dalam ruang 3D, karena tidak ada sumbu yang tersisa untuk bervariasi.

Contoh Kasus

1. Jika kita menetapkan dalam ruang tiga dimensi, maka kita menciptakan bidang di mana semua titik di bidang tersebut memiliki nilai , sementara dan bisa bervariasi.

2. Jika kita menetapkan dan , maka kita mendapatkan garis yang sejajar dengan sumbu-z, karena hanya nilai yang bisa berubah.

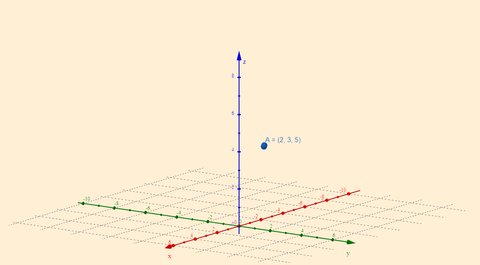
3. Jika kita menetapkan , , dan , maka kita telah menentukan satu titik spesifik di ruang tiga dimensi: .

Kesimpulan:

• 1 komponen titik (misalnya, ) akan membentuk sebuah bidang yang sejajar dengan dua sumbu lainnya.
• 2 komponen titik (misalnya, dan ) akan membentuk sebuah garis yang sejajar dengan satu sumbu lainnya.
• 3 komponen titik (misalnya, , , dan ) akan menunjukkan titik spesifik di ruang tiga dimensi.

Rumus pada Dimensi 2 yang Masih Relevan di Dimensi 3

Beberapa rumus dalam sistem koordinat dua dimensi tetap berlaku di tiga dimensi, hanya dengan sedikit penyesuaian. Berikut adalah dua di antaranya yang masih sangat relevan:

1. Rumus Jarak antara Dua Titik: Dalam dua dimensi, jarak antara dua titik dan dihitung menggunakan rumus Pythagoras:

Did you know?

Di dalam tiga dimensi, rumus ini diperluas dengan menambahkan komponen z, sehingga jarak antara dua titik dan dihitung dengan rumus:

Contoh: Misalkan kita ingin menghitung jarak antara dua titik dan . Dengan menggunakan rumus ini, kita mendapatkan:

1. Persamaan Standar Bola: Sama seperti dalam dua dimensi di mana lingkaran direpresentasikan dengan persamaan:

Did you know?

Dalam tiga dimensi, bentuk bola bisa direpresentasikan dengan persamaan standar:

Di sini, adalah pusat bola dan adalah jari-jarinya.

Contoh: Jika bola memiliki pusat di dan jari-jarinya 5, maka persamaan bola tersebut adalah: